الگوریتم‌های مرتب‌سازی- پرکاربردی ترین الگوریتم‌های مرتب‌سازی

الگوریتم‌های مرتب‌سازی  (Sorting Algorithms)
 یکی از بنیادی‌ترین و در عین حال جذاب‌ترین مباحث در علوم کامپیوتر هستند. این الگوریتم‌ها مانند چیدمان کتاب‌ها در کتابخانه یا مرتب کردن کارت‌های بازی در دست شما عمل می‌کنند.

در ادامه، سفری جامع و جذاب به دنیای مرتب‌سازی خواهیم داشت.

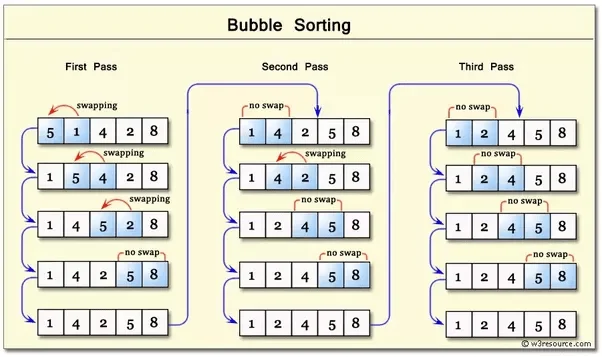
1. مرتب‌سازی حبابی (Bubble Sort)

ایده اصلی: تصور کنید در یک استخر، حباب‌های سنگین به ته می‌روند و حباب‌های سبک به سطح آب می‌آیند.

• روش کار: الگوریتم از ابتدای لیست شروع کرده و هر دو عنصر مجاور را با هم مقایسه می‌کند. اگر ترتیب آن‌ها غلط باشد، جایشان را عوض می‌کند. این کار را آن‌قدر تکرار می‌کند تا بزرگترین عنصر مانند یک حباب به انتهای لیست برسد.
• جذابیت: ساده‌ترین الگوریتم است، اما برای لیست‌های بزرگ بسیار کند عمل می‌کند.
• پیچیدگی زمانی O(n2)O(n2) :

#include <iostream>

#include <vector>

using namespace std;

int main() {

    vector<int> a = {64, 34, 25, 12, 22, 11, 90};

    int n = a.size();

    for (int i = 0; i < n - 1; ++i) {

        bool swapped = false;

        for (int j = 0; j < n - 1 - i; ++j) {

            if (a[j] > a[j + 1]) {

                int t = a[j];

                a[j] = a[j + 1];

                a[j + 1] = t;

                swapped = true;

            }

        }

        if (!swapped) break;

    }

    cout << "qable moratabsazi: 64, 34, 25, 12, 22, 11, 90 \n";

    cout << "bade moratabsazi: ";

    for (int x : a) cout << x << " ";

    cout << endl;

    return 0;
}

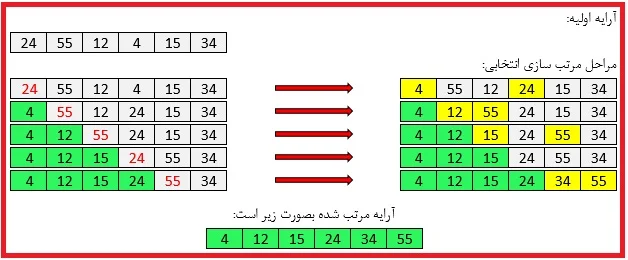
2. مرتب‌سازی انتخابی (Selection Sort)

ایده اصلی: گلچین کردن!

• روش کار: الگوریتم کل لیست را می‌گردد، کوچک‌ترین عنصر را پیدا می‌کند و آن را در اولین جایگاه قرار می‌دهد. سپس در میان باقی‌مانده‌ها دوباره کوچک‌ترین را پیدا کرده و در جایگاه دوم می‌گذارد.
• جذابیت: تعداد جابه‌جایی‌ها در این روش بسیار کم است (O(n)O(n))، اما تعداد مقایسه‌ها همچنان زیاد است.
• پیچیدگی زمانی O(n2)O(n2) :

#include <iostream>

#include <vector>

using namespace std;

int main() {

    vector<int> a = {64, 25, 12, 22, 11};

    int n = a.size();

    for (int i = 0; i < n - 1; ++i) {

        int minIdx = i;

        for (int j = i + 1; j < n; ++j) {

            if (a[j] < a[minIdx]) minIdx = j;

        }

        if (minIdx != i) {

            int t = a[i];

            a[i] = a[minIdx];

            a[minIdx] = t;

        }

    }

         cout << "qable moratabsazi: 64, 25, 12, 22, 11\n";

    cout << "bade moratabsazi: ";

    for (int x : a) cout << x << " ";

    cout << endl;

    return 0;

}

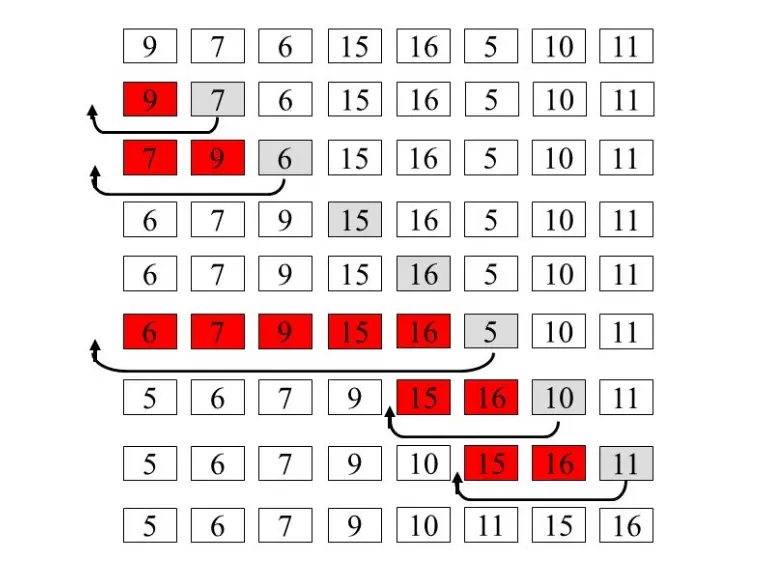
3. مرتب‌سازی درجی (Insertion Sort)

ایده اصلی: شبیه به مرتب کردن کارت‌های بازی در دست.

• روش کار: شما یک کارت را برمی‌دارید و آن را در جای درست خود در میان کارت‌هایی که قبلاً مرتب کرده‌اید، "درج" می‌کنید.
• جذابیت: برای لیست‌های کوچک یا لیست‌هایی که تقریباً مرتب هستند، فوق‌العاده سریع عمل می‌کند.
• پیچیدگی زمانی O(n2)O(n2) ) :در بهترین حالت  O(n)O(n))

#include <iostream>

#include <vector>

using namespace std;

int main() {

    vector<int> a = {12, 11, 13, 5, 6};

    int n = a.size();

    for (int i = 1; i < n; ++i) {

        int key = a[i];

        int j = i - 1;

        while (j >= 0 && a[j] > key) {

            a[j + 1] = a[j];

            --j;

        }

        a[j + 1] = key;

    }

        cout << "qable moratabsazi: 12, 11, 13, 5, 6\n";

cout << "bade moratabsazi: ";

    for (int x : a) cout << x << " ";

    cout << endl;

    return 0;

}

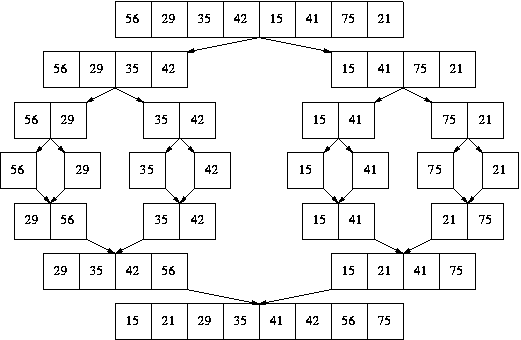
4. مرتب‌سازی ادغامی (Merge Sort)

ایده اصلی: تفرقه بینداز و حکومت کن (Divide and Conquer).

• روش کار: لیست را به دو نیمه تقسیم می‌کند، هر نیمه را به صورت بازگشتی مرتب می‌کند و در نهایت دو نیمه مرتب شده را با هم "ادغام" می‌کند.
• جذابیت: بسیار پایدار و قابل پیش‌بینی است. فرقی نمی‌کند لیست شما چقدر به‌هم‌ریخته باشد، این الگوریتم همیشه با سرعت خوبی عمل می‌کند.

پیچیدگی زمانی: (nlog⁡n)O(nlogn)

 #include <iostream>

#include <vector>

#include <functional>

using namespace std;

int main() {

    vector<int> a = {38, 27, 43, 3, 9, 82, 10};

    int n = a.size();

    // merge ساده به صورت lambda

    auto merge = [&](int l,int m,int r) {

        int n1 = m - l + 1;

        int n2 = r - m;

        vector<int> L(n1), R(n2);

        for (int i = 0; i < n1; ++i) L[i] = a[l + i];

        for (int j = 0; j < n2; ++j) R[j] = a[m + 1 + j];

        int i = 0, j = 0, k = l;

        while (i < n1 && j < n2) {

            if (L[i] <= R[j]) a[k++] = L[i++];

            else a[k++] = R[j++];

        }

        while (i < n1) a[k++] = L[i++];

        while (j < n2) a[k++] = R[j++];

    };

        function<void(int,int)> mergeSort = [&](int l,int r) {

        if (l >= r) return;

        int m = l + (r - l) / 2;

        mergeSort(l, m);

        mergeSort(m + 1, r);

        merge(l, m, r);

    };

    mergeSort(0, n - 1);

    cout << "qable moratabsazi: 38, 27, 43, 3, 9, 82, 10\n";

        cout << "bade moratabsazi: ";

    for (int x : a) cout << x << " ";

    cout << endl;

    return 0;

}

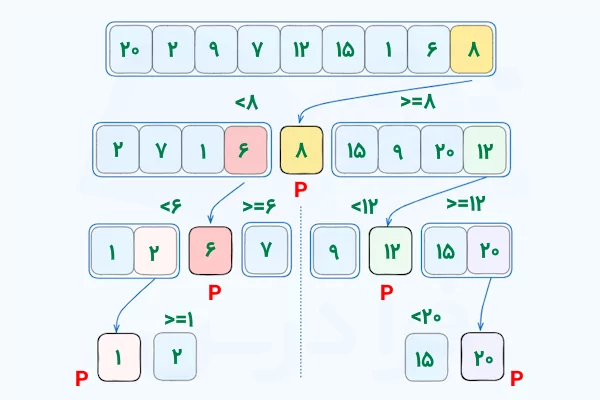
5. مرتب‌سازی سریع (Quick Sort)

ایده اصلی: انتخاب یک محور (Pivot).

• روش کار: یک عنصر به نام "محور" انتخاب می‌شود. اعداد کوچک‌تر به سمت چپ و اعداد بزرگ‌تر به سمت راست محور منتقل می‌شوند. سپس همین فرآیند برای دو طرف تکرار می‌شود.
• جذابیت: در دنیای واقعی، معمولاً سریع‌ترین الگوریتم مرتب‌سازی مبتنی بر مقایسه است. اکثر کتابخانه‌های زبان‌های برنامه‌نویسی از نسخه‌ای از این الگوریتم استفاده می‌کنند.
• پیچیدگی زمانی: متوسط O(nlog⁡n)O(nlogn)

#include <iostream>

#include <vector>

#include <functional>

using namespace std;

int main() {

    vector<int> a = {38, 27, 43, 3, 9, 82, 10};

    int n = a.size();

    // partition به صورت lambda

    auto partition = [&](int low,int high) -> int {

        int pivot = a[high];

        int i = low - 1;

        for (int j = low; j <= high - 1; ++j) {

            if (a[j] <= pivot) {

                ++i;

                swap(a[i], a[j]);

            }

        }

        swap(a[i + 1], a[high]);

        return i + 1;

    };

        std::function<void(int,int)> quickSort = [&](int low,int high) {

        if (low < high) {

            int pi = partition(low, high);

            quickSort(low, pi - 1);

            quickSort(pi + 1, high);

        }

    };

    quickSort(0, n - 1);

    cout << "qable moratabsazi: 38, 27, 43, 3, 9, 82, 10\n";

        cout << "bade moratabsazi: ";

    for (int x : a) cout << x << " ";

    cout << endl;

    return 0;

}

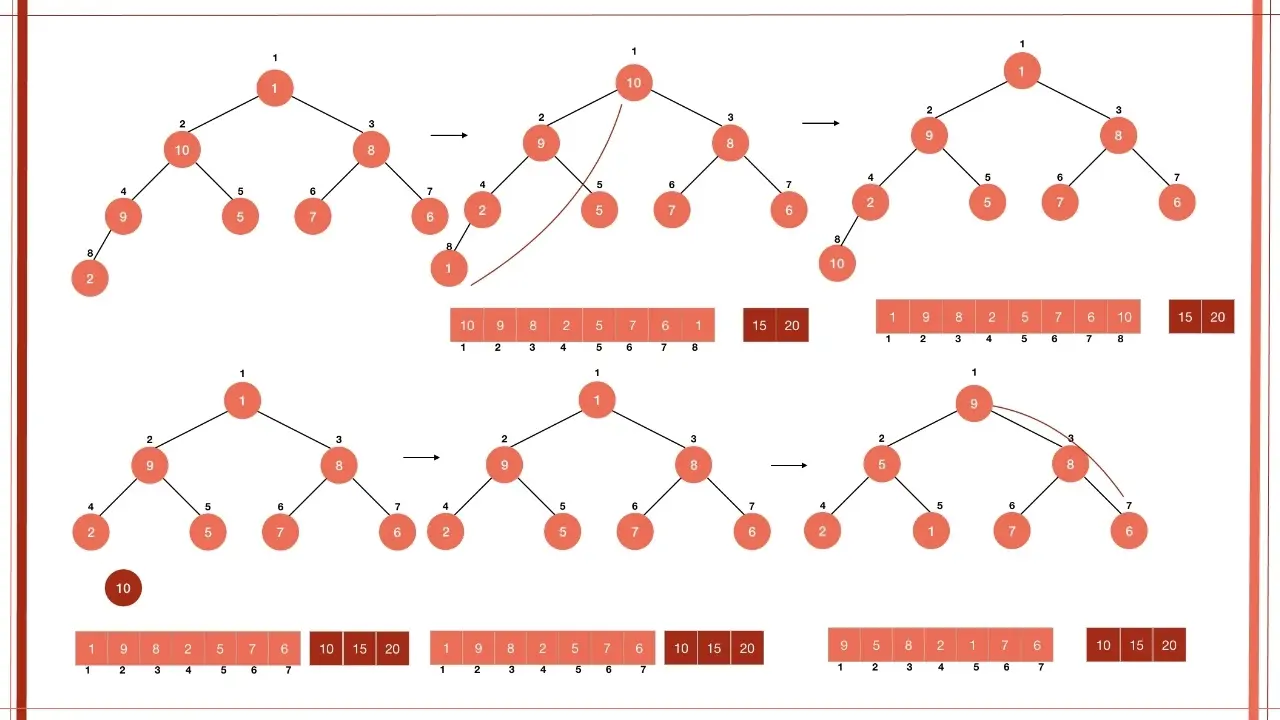
6. مرتب‌سازی هرمی  (Heap Sort)

ایده اصلی: استفاده از ساختار داده "هرم" یا "درخت".

• روش کار: اعداد را در یک درخت باینری (Max-Heap) قرار می‌دهد که در آن ریشه همیشه بزرگترین عضو است. ریشه را حذف کرده و در انتهای لیست قرار می‌دهد و درخت را بازسازی می‌کند.
• جذابیت: مانند Merge Sort تضمین زمانی دارد اما برخلاف آن، نیاز به حافظه اضافی ندارد.
• پیچیدگی زمانی O(nlog⁡n)O(nlogn) :

#include <iostream>

#include <vector>

#include <functional>

using namespace std;

int main() {

    vector<int> a = {38, 27, 43, 3, 9, 82, 10};

    int n = a.size();

    // heapify (سازماندهی زیردرخت به صورت max-heap) به صورت lambda

    auto heapify = [&](int heap_size,int i) {

        int largest = i;

        int l = 2 * i + 1;

        int r = 2 * i + 2;

        if (l < heap_size && a[l] > a[largest]) largest = l;

        if (r < heap_size && a[r] > a[largest]) largest = r;

        if (largest != i) {

            swap(a[i], a[largest]);

            // بازگشت بازگشتی با همان لامبدا: استفاده از std::function لازم است

            std::function<void(int,int)> heapify_rec = [&](int hs,int idx) {

                int largest2 = idx;

                int l2 = 2 * idx + 1;

                int r2 = 2 * idx + 2;

                if (l2 < hs && a[l2] > a[largest2]) largest2 = l2;

                if (r2 < hs && a[r2] > a[largest2]) largest2 = r2;

                if (largest2 != idx) {

                    swap(a[idx], a[largest2]);

                    heapify_rec(hs, largest2);

                }

            };

            heapify_rec(heap_size, largest);

        }

    };

    // ساختن max-heap

    for (int i = n / 2 - 1; i >= 0; --i) heapify(n, i);

    // استخراج عناصر از heap یکی‌یکی

    for (int i = n - 1; i > 0; --i) {

        swap(a[0], a[i]);           // بزرگ‌ترین را به انتها بفرست

        heapify(i, 0);             // heapify روی سایز کم‌شده

    }

    cout << "qable moratabsazi: 38, 27, 43, 3, 9, 82, 10\n";

        cout << "bade moratabsazi: ";

    for (int x : a) cout << x << " ";

    cout << endl;

    return 0;

}

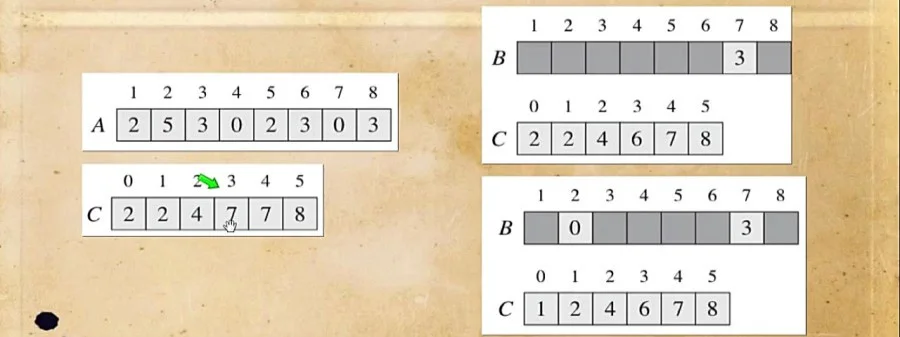
7. مرتب‌سازی شمارشی (Counting Sort)

ایده اصلی: بدون مقایسه! (فقط برای اعداد صحیح).

• روش کار: به جای مقایسه، تعداد تکرار هر عدد را می‌شمارد. اگر بدانید 5 تا عدد "2" دارید، مستقیماً 5 بار عدد 2 را در لیست خروجی می‌نویسید.
• جذابیت: بسیار سریع‌تر از الگوریتم‌های قبلی است، اما فقط زمانی کار می‌کند که محدوده اعداد (Range) را بدانید.
• پیچیدگی زمانی O(n+k)O(n+k) :

#include <iostream>

#include <vector>

#include <algorithm> // for max_element

using namespace std;

int main() {

    vector<int> a = {4, 2, 2, 8, 3, 3, 1};

    int n = a.size();

    int max_val = *max_element(a.begin(), a.end());

        auto countingSort = [&](vector<int>&arr) {

        int m = max_val + 1;

        vector<int> count(m, 0);

        for (int x : arr) ++count[x];

        for (int i = 1; i < m; ++i) count[i] += count[i - 1];

        vector<int> output(n);

        for (int i = n - 1; i >= 0; --i) {

            int val = arr[i];

            output[--count[val]] = val;

        }

               for (int i = 0; i < n; ++i) arr[i] = output[i];

    };

    countingSort(a);

        cout << "qable moratabsazi: 4, 2, 2, 8, 3, 3, 1\n";

    cout << "bade moratabsazi: ";    for (int x : a) cout << x << " ";

    cout << endl;

    return 0;

{

8. مرتب‌سازی رادیکس (Radix Sort)

ایده اصلی: مرتب‌سازی بر اساس رقم.

• روش کار: ابتدا اعداد را بر اساس رقم یکان مرتب می‌کند، سپس دهگان، سپس صدگان و... تا کل عدد مرتب شود.
• جذابیت: برای مرتب‌سازی حجم عظیمی از اعداد با تعداد ارقام ثابت، معجزه می‌کند.

#include <iostream>

#include <vector>

#include <algorithm>

using namespace std;

int main() {

    vector<int> a = {170, 45, 75, 90, 802, 24, 2, 66};

    int n = a.size();

    int max_val = *max_element(a.begin(), a.end());

    if (max_val == 0) {

        cout << "بعد از مرتب‌سازی رادیکس: 0\n";

        return 0;

    }

        auto countingByDigit = [&](intexp) {

        vector<int> output(n);

        int k = 10;

        vector<int> count(k, 0);

        for (int i = 0; i < n; ++i) {

            int digit = (a[i] / exp) % 10;

            ++count[digit];

        }

        for (int i = 1; i < k; ++i) count[i] += count[i - 1];

        for (int i = n - 1; i >= 0; --i) {

            int digit = (a[i] / exp) % 10;

            output[--count[digit]] = a[i];

        }

        for (int i = 0; i < n; ++i) a[i] = output[i];

    };

    for (int exp = 1; max_val / exp > 0; exp *= 10) {

        countingByDigit(exp);

    }

       cout << "qable moratabsazi: 170, 45, 75, 90, 802, 24, 2, 66\n";

    cout << "bade moratabsazi: ";    

    for (int x : a) cout << x << " ";

    cout << endl;

    return 0;

}

کدام یک برنده است؟

انتخاب الگوریتم بستگی به شرایط دارد:

• اگر حافظه کم دارید Quick Sort :یا Heap Sort
• اگر پایداری (حفظ ترتیب عناصر مساوی) مهم است Merge Sort .
• اگر لیست کوچک یا نیمه‌مرتب است Insertion Sort .
• اگر سرعت مطلق در اعداد صحیح می‌خواهید Counting Sort .

دنیای مرتب‌سازی به ما می‌آموزد که برای هر مسئله‌ای، یک "نظم" بهینه وجود دارد؛ فقط باید ابزار درست را انتخاب کرد!